Bayesian inference in quantum chemistry
Small introduction
In the field of computational quantum chemistry, scientists model molecules using foundational physical models like density functional theory. These methods are electronic, which according to our good pal of recent popularity Oppenheimer, is only half the story. Nuclear contributions to the molecular wavefunction include vibrations of the atoms within the molecule. The solution to foundationally accurate molecular simulations is as simple as computing the electronic energies of all possible atomic configurations, and assessing the likelihood of finding the molecule in each configuration. The problem is that there’s no computationally tractable way to visit every single configuration and run a computation. If this sounds like the setup to a Bayesian problem, you’re paying attention.
Take a look at methanol, six atoms, and 6 3 = 18 input variables, one for each Cartesian coordinate. Each configuration vector is a single input to the a ab initio predictor, . is realistically constrained to certain spatial values – molecules stay together after all. These can be represented as stretches, bends, and rotations within the molecule, like this:
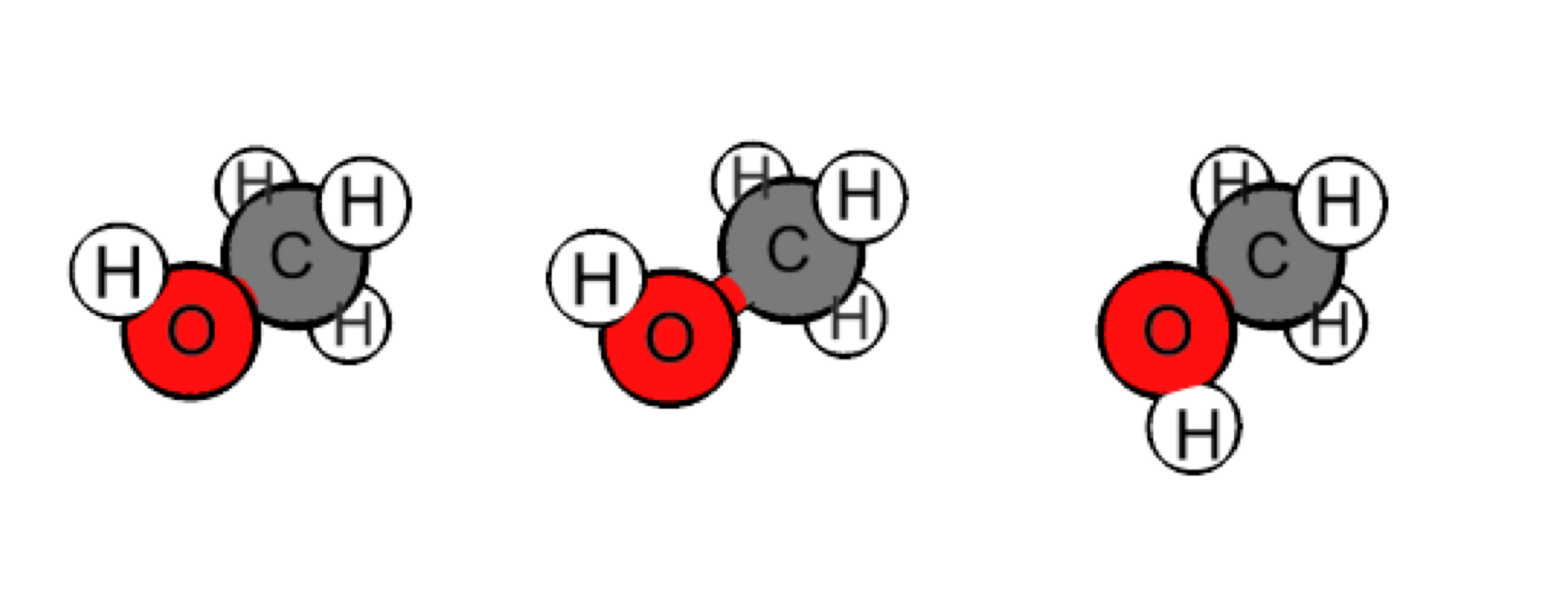
| 16.2364 | 4.55882 | 8.60984 | 17.2446 | 4.35514 | 9.00149 | 15.5804 | 4.89513 | 9.42765 | 15.8392 | 3.63217 | 8.18469 | 16.2648 | 5.5148 | 7.5602 | 16.7107 | 6.32543 | 7.83257 | -115.631 |
| 16.2337 | 4.46458 | 9.10497 | 17.2418 | 4.26089 | 9.10497 | 15.5776 | 4.80088 | 9.53114 | 15.8364 | 3.53793 | 8.28817 | 16.2675 | 5.60905 | 7.72909 | 16.7135 | 6.41968 | 7.83257 | -115.606 |
| 16.2365 | 4.55882 | 8.60984 | 17.2446 | 4.35514 | 9.00149 | 15.5804 | 4.89513 | 9.42765 | 15.8392 | 3.63217 | 8.18469 | 16.2648 | 5.5148 | 7.5602 | 15.5917 | 5.32897 | 6.89489 | -115.629 |
Even with constraints on the internal “relative” positions of the atoms w.r.t. each other (i.e. feature engineering a.k.a. coordinate transformation a.k.a. internal coordinates), visiting every possible input and computing the energy is prohibitively expensive, even when parallelized.
Don’t forget, in silico quantum mechanics simulation requires constructing and diagonalizing a matrix in a finite basis. Even for small molecules like methane, this is severely limited by memory and computation cost.
Further complicating things, classical simulations such as molecular dynamics (glorified Newtonian mechanics) are not actually foundational because molecules are quantum mechanical. The consequences are an inaccurate model (validated on data from laboratory measurements/observations).
Many assumptions simplify the model at the cost of some degree of technical accuracy. One assumption is non-interacting motions, meaning mathematically a molecule’s potential energy is linearly separable.
Then one needs to train just models, one for each axis, and add their result.
The choice of model for is critical. A good place to start is the margins. Collect data for each motion independently, fit the appropriate model, and diagonalize its Hamiltonian matrix (how-to is detailed in previous posts). The matrices are now much smaller under this approximation. This is tractable.
The a priori probability under this approximation is therefore separable. The normalization constant is called the partition function in chemistry.
Probabilistically, a hypothetical molecule with only three motions in the quantum state is the product of three probabilities.
But we can improve. Although we cannot compute the joint probability directly, we can compute the a posteriori probability by updating our priors with new data from the joint distribution.
So for each motion in and quantum number pair
The prior on is what we just defined, so what’s left to obtain the posterior distribution is the likelihood of a given outcome (). This is easy, considering all energies are distributed in the canonical ensemble with an exponential likelihood. Therefore, the likelihood of an observation is